Questões de Matemática da INEP do ENEM

Em um laboratório, cientistas observaram o crescimento de uma população de bactérias submetida a uma dieta magra em fósforo, com generosas porções de arsênico. Descobriu-se que o número de bactérias dessa população, após t horas de observação, poderia ser modelado pela função exponencial N(t) = N₀e^kt, em que N₀ é o número de bactérias no instante do início da observação (t = 0) e representa uma constante real maior que 1, e k é uma constante real positiva.
Sabe-se que, após uma hora de observação, o número de bactérias foi triplicado. Cinco horas após o início da observação, o número de bactérias, em relação ao número inicial dessa cultura, foi

Uma formiga encontra-se no ponto X, no lado externo de um copo que tem a forma de um cilindro reto. No lado interno, no ponto V, existe um grão de açúcar preso na parede do copo. A formiga segue o caminho XYZWV (sempre sobre a superfície lateral do copo), de tal forma que os trechos ZW e WV são realizados na superfície interna do copo. O caminho XYZWV é mostrado na figura.

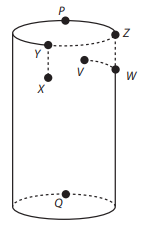
Sabe-se que: os pontos X, V, W se encontram à mesma distância da borda; o trajeto WV é o mais curto possível; os trajetos XY e ZW são perpendiculares à borda do copo; e os pontos X e V se encontram diametralmente opostos.
Supondo que o copo é de material recortável, realiza-se um corte pelo segmento unindo P a Q, perpendicular à borda do copo, e recorta-se também sua base, obtendo então uma figura plana. Desconsidere a espessura do copo.
Considerando apenas a planificação da superfície lateral do copo, a trajetória da formiga é

Um jardineiro cultiva plantas ornamentais e as coloca à venda quando estas atingem 30 centímetros de altura. Esse jardineiro estudou o crescimento de suas plantas, em função do tempo, e deduziu uma fórmula que calcula a altura em função do tempo, a partir do momento em que a planta brota do solo até o momento em que ela atinge sua altura máxima de 40 centímetros. A fórmula é h = 5·log₂ (t + 1), em que t é o tempo contado em dia e h, a altura da planta em centímetro.
A partir do momento em que uma dessas plantas é colocada à venda, em quanto tempo, em dia, ela alcançará sua altura máxima?

No desenvolvimento de um novo remédio, pesquisadores monitoram a quantidade Q de uma substância circulando na corrente sanguínea de um paciente, ao longo do tempo t. Esses pesquisadores controlam o processo, observando que Q é uma função quadrática de t. Os dados coletados nas duas primeiras horas foram:

t (hora) 0 1 2 Q (miligrama) 1 4 6


Para decidir se devem interromper o processo, evitando riscos ao paciente, os pesquisadores querem saber, antecipadamente, a quantidade da substância que estará circulando na corrente sanguínea desse paciente após uma hora do último dado coletado
Nas condições expostas, essa quantidade (em miligrama) será igual a

Na anestesia peridural, como a usada nos partos, o médico anestesista precisa introduzir uma agulha nas costas do paciente, que atravessará várias camadas de tecido até chegar a uma região estreita, chamada espaço epidural, que envolve a medula espinhal. A agulha é usada para injetar um líquido anestésico, e a força que deve ser aplicada à agulha para fazê-la avançar através dos tecidos é variável.
A figura é um gráfico do módulo F da força (em newton) em função do deslocamento x da ponta da agulha (em milímetro) durante uma anestesia peridural típica.
Considere que a velocidade de penetração da agulha deva ser a mesma durante a aplicação da anestesia e que a força aplicada à agulha pelo médico anestesista em cada ponto deve ser proporcional à resistência naquele ponto.

HALLIDAY, D.; RESNICK, R. Fundamentos de física. Rio de Janeiro: lTC, 2008.
Com base nas informações apresentadas, a maior resistência à força aplicada observa-se ao longo do segmento