Analise as seguintes afirmativas com relação à análise entre variáveis aleatórias:
I. As técnicas de regressão e correlação em hidrologia são utilizadas em diversos casos como a previsão e regionalização hidrológicas.
II. A correlação entre duas variáveis aleatórias é uma técnica pouco utilizada em hidrologia devido ao caráter aleatório das amostras.
III. Variações temporais nos níveis d'água médios diários de uma seção fluvial de uma grande bacia hidrográfica, monitorada pelas médias aritméticas das leituras em réguas linimétricas tomadas às 8h e 18h de cada dia, podem ser consideradas variáveis hidrológicas aleatórias.
Está CORRETO o que afirma em:

Com referência a essas variáveis, julgue os próximos itens.
Se T = X + Y representa o total diário de notificações de incidentes de segurança registrado nas referidas redes de computadores, então Var(T) $ Var(X) + Var(Y).Um processo auto regressivo de ordem p, AR(p), pode ser escrito da forma:
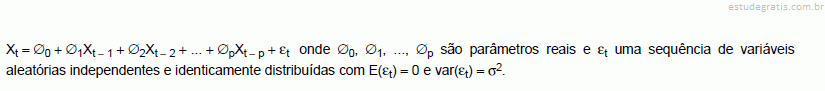
Corresponde a um processo AR(p) estacionário:
Seja a variável X = (X1, X2, X3) uma distribuição normal com média μ = (0, 0, 0) e matriz de covariância
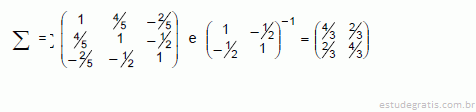
O coeficiente de correlação entre X1 e (X2, X3) é dado por
Pode-se demonstrar que se X for uma variável aleatória contínua com função densidade de probabilidade f(x) e função de densidade acumulada F(x), então a variável aleatória U = F(x) tem distribuição uniforme no intervalo [0,1]. Considere uma variável aleatória Y com uma distribuição exponencial com média 0,5.
Foram simulados três valores de uma distribuição uniforme com o seguinte resultado: u1 = 0,66; u2 = 0,42; u3 = 0,18.
Dado que In(0,34) = −1,79; In (0,58) = − 0,545; In (0,82) = − 0,2 e utilizando as informações disponíveis, é possível gerar três valores da variável aleatória Y. A soma aproximada desses três valores gerados é